Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://vorhilfe.de/vorkurszettel?id=10
| Sigrid Sprock Marc O. Sandlus | www.matheraum.de Vorbereitung auf das Zentralabitur in Mathematik in NRW Aufgabenblatt 2 Abgabe: Fr 10.07.2009 16:00 | 06.10.2006 |
| Aufgabe 18 | ||
Gegeben sind die Gerade g durch den Punkt P(2 | 1 | -1) und den Richtungsvektor 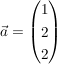 und die Gerade und die Gerade 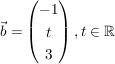 . .
a) Bestimmen Sie t so, dass sich die beiden Geraden schneiden, und berechnen Sie die Koordinaten des Schnittpunktes S. (Ergebnis: t = -1; S( 6 | 9 | 7) ). b) Bestimmen Sie die Koordinaten der Punkte auf der Geraden g, die von Q die Entfernung (Ergebnis: A(6 | 9 | 7) = S, B(4 | 5 | 3) ) c) d) 1. Geben Sie eine Koordinatengleichung der durch die Geraden g und | ||
© Copyright 2003-25 www.vorhilfe.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.