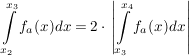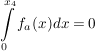Vorhilfe - Kostenlose Kommunikationsplattform für gegenseitige Hilfestellungen
URL: http://vorhilfe.de/vorkurszettel?id=4
Sigrid Sprock
Marc O. Sandlus		www.matheraum.de
Vorbereitung auf das Zentralabitur in Mathematik in NRW
Aufgabenblatt 1
Abgabe: Fr 10.07.2009 16:00		22.09.2006
Aufgabe 1
Flächenstrategien

Gegeben sind die Funktionen $ f_a $ mit $ f_a(x)=\bruch1{8a^3}(x^4-8a^2x^2)+2,\ x\in\IR,\ a\in\IR^{\not=0} $.

a) Untersuchen Sie für a > 0 den Graphen zu $ f_a $ auf Symmetrie sowie auf sein Verhalten für $ |x|\to\infty $. Bestimmen Sie die Extrem- und Wendepunkte des Graphen in Abhängigkeit von a.

b)
1. Bestimmen Sie denjenigen Wert von a, für den der zu $ f_a $ gehörende Graph einen Extrempunkt auf der x-Achse hat.

2. Beschreiben Sie den Verlauf der Graphen für negative Werte a und begründen Sie Ihre Aussage.

3. Bestimmen Sie die Anzahl der Nullstellen von f in Abhängigkeit von a.

4. Ermitteln Sie alle Werte für a, so dass der Graph zu $ f_a $ durch den Punkt P( 2 | 0 ) verläuft.

5. Alle Graphen in der Zeichnung unten gehören zur Schar $ f_a $. Geben Sie jeweils das passende a an bzw. den Bereich, aus dem der zugehörige Wert von a stammt, und begründen Sie Ihre Zuordnung.

[Dateianhang]


c) Es soll die folgende Problemstellung bearbeitet werden:
"Bestimmen Sie den Wert von a (a > 1), für den der Inhalt der vom Graphen zu $ f_a $ und der x-Achse oberhalb der x-Achse eingeschlossenen Fläche gleich dem Inhalt der Flächen ist, die die x-Achse und der Graph unterhalb der x-Achse umschließen."


Zur Lösung werden die Vorschläge V 1 und V 2 gemacht:

V1: Ich bestimme die Nullstellen $ x_1, x_2, x_3, x_4 $ mit $ x_1 < x_2 < x_3 < x_4 $ und löse die Gleichung
$ \integral_{x_2}^{x_3} f_a(x) dx=2\cdot{}\left|\integral_{x_3}^{x_4} f_a(x)dx\right| $.


V2: Ich bestimme die Nullstellen $ x_1, x_2, x_3, x_4 $ mit $ x_1 < x_2 < x_3 < x_4 $ und löse die Gleichung
$ \integral_{0}^{x_4} f_a(x)dx=0 $.

Beurteilen Sie diese beiden Vorschläge.
© Copyright 2003-24 www.vorhilfe.de
Der Inhalt dieser Seite kann -- sofern nicht anders lautend gekennzeichnet -- durch jedermann gemäß den Bestimmungen der Lizenz für Freie Inhalte genutzt werden.