FaktorhalbgruppeDefinition Faktorhalbgruppe
Schule
Universität
Es sei 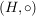 eine Halbgruppe und eine Halbgruppe und 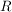 eine verträgliche Äquivalenzrelation auf eine verträgliche Äquivalenzrelation auf 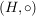 . Dann ist die Menge der Äquivalenzklassen . Dann ist die Menge der Äquivalenzklassen
![$ H/R=\{[a]_R\, \vert\, a \in H\} $ $ H/R=\{[a]_R\, \vert\, a \in H\} $](/teximg/5/4/00387145.png)
zusammen mit der durch
![$ [a]_R \circ [b]_R := [a \circ b]_R $ $ [a]_R \circ [b]_R := [a \circ b]_R $](/teximg/6/4/00387146.png)
definierten Verknüpfung eine Halbgruppe.
Man nennt diese Halbgruppe 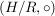 die Faktorhalbgruppe (oder Restklassenhalbgruppe) von die Faktorhalbgruppe (oder Restklassenhalbgruppe) von 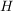 nach nach 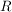 (oder von (oder von 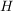 modulo modulo 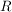 ). ).
Bemerkung
Es hat sich als sehr zweckmäßig erwiesen, für die Verknüpfungen in 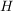 und die dadurch induzierte Verknüpfung in und die dadurch induzierte Verknüpfung in 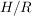 dieselben Zeichen zu verwenden. dieselben Zeichen zu verwenden.
Beispiel
Im Bereich 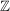 der ganzen Zahlen kennen wir die Division mit Rest; d.h. zu der ganzen Zahlen kennen wir die Division mit Rest; d.h. zu 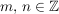 , , 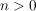 , gibt es eindeutig bestimmte , gibt es eindeutig bestimmte 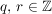 mit mit
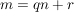 und und 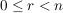 . .
( heißt der Rest.) heißt der Rest.)
Zu 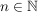 erklären wir eine Relation erklären wir eine Relation 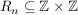 durch durch
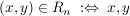 haben bei Division durch haben bei Division durch  den gleichen Rest. den gleichen Rest.
Wie man sieht, ist 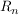 eine Äquivalenzrelation auf eine Äquivalenzrelation auf 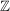 . Anstatt . Anstatt 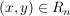 schreibt man üblicherweise schreibt man üblicherweise
(*) 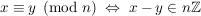 . .
Denn haben  und und  bei Division durch bei Division durch  den gleichen Rest, dann ist den gleichen Rest, dann ist 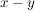 ein Vielfaches von ein Vielfaches von  . Gilt andererseits . Gilt andererseits 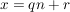 und und 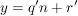 mit mit 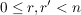 und und 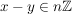 , dann ist auch , dann ist auch 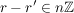 , das geht wegen der Einschränkung , das geht wegen der Einschränkung 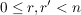 nur für nur für 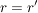 , also , also 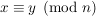 . .
Nun wird gezeigt, dass die Relation "kongruent modulo  " mit " mit 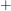 und und  auf auf 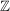 verträglich ist: verträglich ist:
Dafür sei 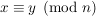 und und 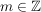 . Wegen (*) ist dann . Wegen (*) ist dann
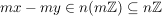 , ,
also:
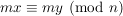 . .
Außerdem gilt trivialerweise
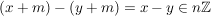 , ,
also auch:
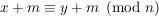 . .
Das zeigt bereits die Verträglichkeit mit 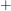 und und  . .
Sei 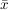 die Äquivalenzklasse die Äquivalenzklasse 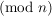 von von 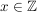 , in diesem Fall Restklasse modulo , in diesem Fall Restklasse modulo  genannt: genannt:
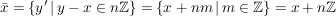 . .
Die Menge der Restklassen wir mit 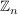 bezeichnet. Da jede Klasse zu genau einem Rest gehört, haben wir bezeichnet. Da jede Klasse zu genau einem Rest gehört, haben wir
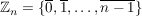 . .
Beachte: 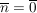 , , 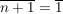 , etc. , etc.
Wegen der Veträglichkeit der Äquivalenzrelationen mit 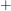 und und  haben wir in kanonischer Weise auf haben wir in kanonischer Weise auf 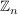 die Verknüpfungen die Verknüpfungen 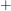 und und  erklärt, nämlich erklärt, nämlich
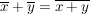
und
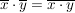 , ,
und 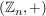 , , 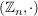 sind Halbgruppen. sind Halbgruppen.
Quelle: K. Meyberg, Algebra Teil 1, Carl Hanser Verlag, 1980, ISBN 3-446-13079-9
|