MaterialForum357 Kurvendiskussion
ganzrationale Funktionen
In diesem Abschnitt wird eine vollständige Kurvendiskussion für eine ganzrationale Funktion durchgeführt. Als Beispielfunktion dient dabei die Funktion
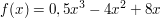
Ganzrationale Funktionen sind allgemein stetig und differenzierbar, sodass man sich über Definitionslücken und Polstellen keine Gedanken machen muss.
Definitionsbereich
Da wie bereits erwähnt keine Polstellen oder Definitionslücken auftreten können gilt für ganzrationale Funktionen:
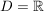
Der Definitionsbereich ist also stets die Menge der reellen Zahlen (solange in der Aufgabenstellung nicht explizit Ausnahmen angegeben sind).
Symmetrieeigenschaften
An ganzrationalen Funktionen lässt sich sehr einfach erkennen ob eine Funktion achsensymmetrisch zur y-Achse oder punktsymmetrisch zum Ursprung ist:
Besitzt die ganzrationale Funktion ausschliesslich gerade Exponenten, so ist die Funktion achsensymmetrisch zur y-Achse.
Besitzt die ganzrationale Funktion ausschliesslich ungeradzahlige Exponenten, so ist die Funktion punktsymmetrisch zum Koordinatenursprung.
Treten sowohl geradzahlige als auch ungeradzahlige Exponenten auf so liegt keine Symmetrie vor.
Schnittpunkte mit den Koordinatenachsen
Den Schnittpunkt mir der y-Achse (y-Achsenabschnitt) erhält man, indem man in die Funktion den x-Wert $ x = 0 $ einsetzt. Für die Beispielfunktion würde gelten:
f(0) = (0,5 * 0) - (4 * 0) + (8 * 0) = 0
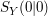
Die Schnittpunkte mit der x-Achse (Nullstellen) kann man mit Hilfe verschiedener Verfahren ermitteln (z.B. p-q-Formel, Mitternachtsformel, quadratische Ergänzung u.s.w.). Für die Beispielfunktion würde gelten:
f(x) = 0
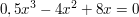
Man kann die Funktion durch Ausklammern in eine quadratische Funktion umformen und gleichzeitig die erste Nullstelle ermitteln:
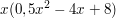
Das ausgeklammerte x wird nur Null, wenn man für x auch Null einsetzt und ein Produkt ist genau dann Null, wenn einer der Faktoren Null ist. Daraus folgt:
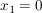
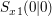
Um die restlichen Nullstellen der Beispielfunktion zu ermitteln kann man nun zum Beispiel die p-q-Formel verwenden, wenn man zuvur den Faktor vor dem ersten x entfernt (alternativ verwendet man die Mitternachtsformel):
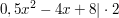
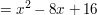
p = -8
q = 16
Es ergibt sich also:
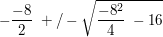
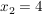
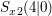
Extrema
Exponentialfunktionen
Logarithmusfunktionen
Integralrechnung
Vektorrechnung
Lösen von linearen Gleichungssystemen (Lineare Algebra)
Analytische Geometrie
Mitteilung des Autors: Artikel unvollständig, wird fortgesetzt !!!
|