Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
Sigrid Sprock
Marc O. Sandlus | www.matheraum.de
Vorbereitung auf das Zentralabitur in Mathematik in NRW
Aufgabenblatt 3
Abgabe: Fr 10.07.2009 16:00 | 20.10.2006 | | Aufgabe 1 | Lipnature
Die Kosmetikfirma lipnature, die sich auf die Produktion von Lippenpflegeprodukten spezialisiert hat, möchte ein neues Firmenlogo entwerfen. Die PR-Abteilung der Firma schlägt dem Vorstand vor, dem neuen Firmenlogo die Form eines Kussmundes zu verleihen.
Die Umrandung der Oberlippe entspricht dem Graphen einer achsensymmetrischen Funktion vierten Grades (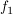 )), welche an der Stelle )), welche an der Stelle  eine Nullstelle und an der Stelle eine Nullstelle und an der Stelle 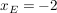 ein relatives Extremum besitzt. Zudem schneidet der Graph die y-Achse an der Stelle ein relatives Extremum besitzt. Zudem schneidet der Graph die y-Achse an der Stelle 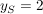
Für die Randlinie der Unterlippe soll der Graph einer quadratischen Funktion 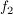 benutzt werden, die durch die Funktionsgleichung benutzt werden, die durch die Funktionsgleichung 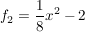 gegeben ist. gegeben ist.
a) Bestimmen Sie die Gleichung der Funktion 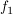 , welche die Randlinie der Oberlippe beschreibt. , welche die Randlinie der Oberlippe beschreibt.
(Zur Kontrolle: 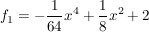 .) .)
b) Bestimmen Sie die gemeinsamen Schnittpunkte der Funktionen 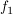 und und 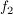 . .
c) Bestimmen Sie alle relativen Extrempunkte sowie Wendepunkte der Funktion 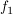 . .
d) Skizzieren Sie das Firmenlogo.
e) Berechnen Sie den Flächeninhalt des Kussmundes.
f) Die PR-Abteilung der Kosmetikfirma schlägt vor, den Firmennamen lipnature als Schriftzug so in den Kussmund zu integrieren, dass er in einem Rechteck zwischen der x-Achse und der Unterlippenrandlinie erscheint. Berechnen Sie die Maße des entsprechenden Rechtecks maximalen Flächeninhalts und geben Sie zudem die Flächenmaßzahl an.
g) Die Fläche des in Teilaufgabe f) ermittelten Rechtecks reicht nicht aus, um den Firmennamen angemessen darin unterbringen zu können. Nun soll die Gleichung, welche die Unterlippenrandlinie beschreibt, derart verändert werden, dass die Nullstellen bei 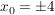 erhalten bleiben, aber die Lage des Scheitelpunkts auf der y-Achse variieren kann. Zeigen Sie, dass alle möglichen Unterlippenrandlinien durch eine allgemeine Funktion erhalten bleiben, aber die Lage des Scheitelpunkts auf der y-Achse variieren kann. Zeigen Sie, dass alle möglichen Unterlippenrandlinien durch eine allgemeine Funktion 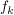 mit mit  ( (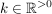 ) wiedergegeben werden. ) wiedergegeben werden. |
Kursdaten anzeigen • Liste aller Vorkurse • Druckansicht
|