PotenzregelAbleitung
Hat eine Funktion f die Form:
so lautet ihre 1. Ableitung
siehe auch Ableitungsregel
Beweis
Der Beweis basiert auf der Beweistechnik der vollständigen Induktion.
Dieser Induktionsbeweis stützt sich auf die Produktregel und die Quotientenregel.
Im ersten Teil des Beweises wird die Behauptung für alle positiven Ganzen Zahlen
bewiesen werden, im zweiten Teil werden dann die negativen Gegenzahlen betrachtet.
1. Fall: Für 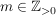 und m:=n mit und m:=n mit 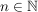 gilt: gilt:
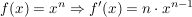
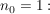
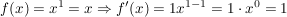 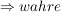 Aussage Aussage
...dies läßt sich durch explizites Nachrechnen, zum Beispiel mit dem Differenzenquotienten, bestätigen.
(siehe Anhang!)
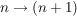 : :
Laut Induktionsvorraussetzung muss für (n+1) folgen:
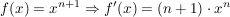 : :
Dieses läßt sich durch einige wenige Umformungen dann im Induktionsschritt zeigen:
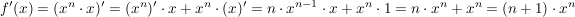
...und dies ist genau die Induktionsbehauptung. Damit ist der erste Teil des Beweises abgeschloßen!
2. Fall: Für alle 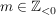 und m:=-n mit und m:=-n mit 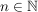 gilt: gilt:
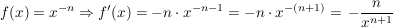
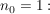
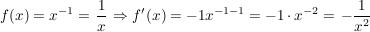 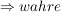 Aussage Aussage
...dies läßt sich durch explizites Nachrechnen, zum Beispiel mit dem Differenzenquotienten, bestätigen. Auch hier ist der Rechenaufwand etwas höher!
(siehe Anhang!)
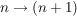 : :
Laut Induktionsvorraussetzung muss für (n+1) folgen:
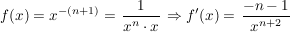
Dies läßt sich ganz analog zum Vorgehen im ersten Teil durchführen, allerdings bedarf es hier wesentlich mehr Rechenarbeit. Los geht´s!
![$ f'(x)=\left (\bruch{1}{x^n\cdot{}x}\right)'=\left \bruch{(1)'\cdot{}(x^n\cdot{}x)-(1)\cdot{}(x^n\cdot{}x)'}{(x^n\cdot{}x)^2} \right=\left \bruch{-(1)\cdot{}(x^n\cdot{}x)'}{(x^{n+1})^2} \right=\left \bruch{-\left[(x^n)'\cdot{}x+x^n\cdot{}(x)'\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[n\cdot{}x^{n-1}\cdot{}x+x^n\cdot{}1\right]}{(x^n\cdot{}x)^2} \right $ $ f'(x)=\left (\bruch{1}{x^n\cdot{}x}\right)'=\left \bruch{(1)'\cdot{}(x^n\cdot{}x)-(1)\cdot{}(x^n\cdot{}x)'}{(x^n\cdot{}x)^2} \right=\left \bruch{-(1)\cdot{}(x^n\cdot{}x)'}{(x^{n+1})^2} \right=\left \bruch{-\left[(x^n)'\cdot{}x+x^n\cdot{}(x)'\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[n\cdot{}x^{n-1}\cdot{}x+x^n\cdot{}1\right]}{(x^n\cdot{}x)^2} \right $](/teximg/4/9/00478494.png)
![$ =\left \bruch{-\left[n\cdot{}x^{n}+x^n\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{x^{2n}\cdot{}x^2 \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{(x^n)^2\cdot{}x^2 \right=\left \bruch{-(n+1)}{x^{n}\cdot{}x^2} \right}=\left \bruch{-n-1}{x^{n+2}} \right} $ $ =\left \bruch{-\left[n\cdot{}x^{n}+x^n\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{(x^n\cdot{}x)^2} \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{x^{2n}\cdot{}x^2 \right=\left \bruch{-\left[(n+1)\cdot{}x^n\right]}{(x^n)^2\cdot{}x^2 \right=\left \bruch{-(n+1)}{x^{n}\cdot{}x^2} \right}=\left \bruch{-n-1}{x^{n+2}} \right} $](/teximg/5/9/00515495.png)
...und nach langer Rechenarbeit zeigt sich: Dies ist wieder die Induktionsbehautung, die im Induktionsschritt gefordert war!
Mit der Beendigung dieses zweiten Teils ist Behauptung nun komplett gezeigt! Fertig!
q.e.d.
Anhang:
An dieser Stelle soll nun noch die Induktionsvorraussetzung des ersten (obgleich diese Aussage trivial ist) und des zweiten Teils rechnerisch gezeigt werden.
Verwendung der Differenzenquotienten gibt...
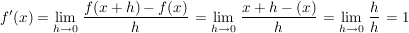
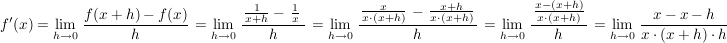
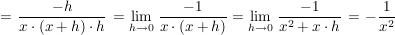
Integration
Integral der Potenzfunktion:
siehe auch Formeln Integralrechnung
|